Modelowanie Procesów Poznawczych

Wstęp i krzywa psychometryczna

W wyniku eksperymentów behawioralnych zbieramy dane dostarczane przez uczestników badań. Mogą być to czasy reakcji, poprawność odpowiedzi, deklarowane pobudzenie emocjonalne i wiele innych. Możemy w myśl standardowego podejścia statystycznego np. porównywać czy w danej grupie badanych średnia danej miary jest większa.

Możemy także spróbować zamodelować dany proces poznawczy tworząc model generatywny, który jest w stanie oddtowrzyć nam zaobserwowane dane. Takie podejście ma kilka przewag nad podejściem standardowym. Po pierwsze, tworząc model potrafiący odtorzyć nam zaaobserwowane dane, jesteśmy w stanie wnioskować na temat samego procesu. Możemy proponować wiele takich modeli i sprawdzać, który jest w stanie najlepiej odtworzyć obserwowane dane i na tej podstawie domniemywać, że podobny mechanizm poznawczy ma miejsce w umyśle człowieka. Po drugie, obserwowane dane mogą być mieszanką kilku procesów poznawczych, a uzycie modelu pozwala je nam od siebie odseparować.

Użycie modelu pozwala nam na wnioskowanie o ukrytych stanach alpha, beta i theta, których nie obserwujemy bezpośrednio w wyniku eksperymentu.

Weźmy jako przykład krzywą psychometryczną. Modeluje ona związek pomiędzy charakterystyką fizyczną bodźca a kategoryzacją tego bodźca przez badanego. Częstym wyborem do modelowania krzywej psychometrycznej jest funkcja logistyczna.

Wyobraźmy sobie badanie, w którym badananemu jest najpier zaprezentowany standarodowy obiekt o długości 100cm, a następnie 401 obiektów różnej długości. Zadaniem badanego jest zdecydowanie czy prezentowany obiekt jest dłuższy czy krótszy od standardowego. Prawdopodobieństwo, że badany określi obiekt jako dłuższy zamodeluje funkcją logistyczną.

library(ggplot2)

stimulus = seq(50,150, by = 0.25)
theta = rep(NA,401)
y = rep(NA,401)
nTrials = 401
standard = 100
alpha = 0
beta = 8
theta = 1/(1+exp(-(stimulus-standard-alpha)/beta))
y = rbinom(401,1,theta) # 0 - badany określił bodziec jako krótszy, 1 - jako dłuższy

dat = data.frame(stimulus,y, check.names = F)

ggplot(dat, mapping = aes(x = stimulus, y = y)) +
  geom_point() + 
  geom_function(fun = function(x){1/(1+exp(-(x-standard-alpha)/beta))}, colour = "blue") +
  xlab("Stimulus Size") + 
  ylab("Shorter\\Longer")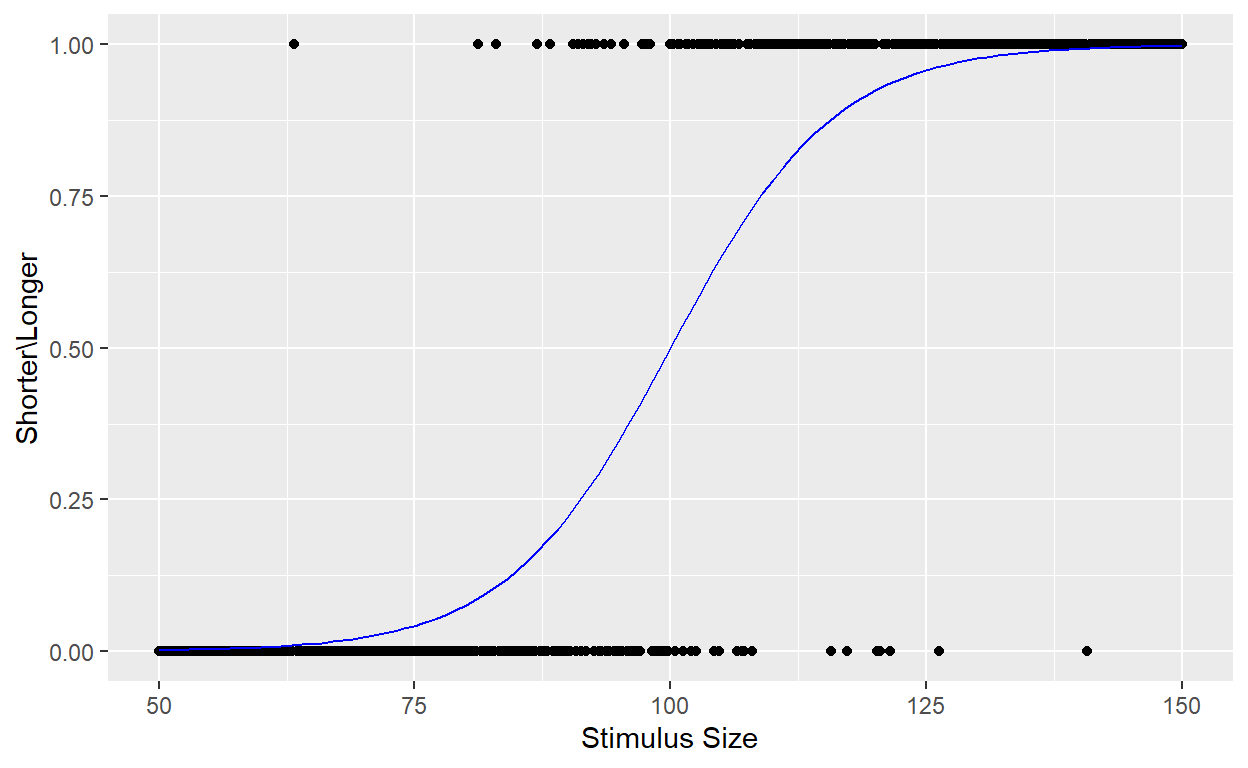

By wyestymować z danych parametry funcji, mogę posłużyć się podejściem bayesowskim.

library(tidyverse)
library(rjags)
library(coda)
library(MCMCvis)

m1 <- "model{
# Likelihood
for (trial in 1:length(y)){
theta[trial] = 1/(1+exp(-(stimulus[trial]-100-alpha)/beta))
y[trial] ~ dbern(theta[trial])
}

# Priors
alpha ~ dnorm(0,1/50^2)
beta ~ dnorm(0,1/100^2)T(0,)
}"

# what parameters we want to track
params = c("alpha", "beta")
# compile model
jmod = jags.model(file = textConnection(m1), data = as.list(dat,nTrials),
n.chains = 4, inits = NULL, n.adapt = 100, quiet = T)
# iterate through jmod for the extent of the burn-in
update(jmod, n.iter=1000, by=1)
# draw samples from the posterior for params
post = coda.samples(jmod, params, n.iter = 4000, thin = 1)
# diagnostic evaluation of posterior samples
MCMCsummary(post, params = c("alpha", "beta"))[,1:6]

           mean        sd      2.5%        50%    97.5% Rhat
alpha -0.371926 1.4082310 -3.097343 -0.3811221 2.407164    1
beta   7.809072 0.8140868  6.354738  7.7564531 9.538688    1

Odzyskałem parametry. Ale zaraz, podobny efekt mógłbym osiągnąć używając zwykłej regresji logistycznej. Dlatego teraz skomplikujmy problem. Uczestnicy badań nie są w każdym trialu skpupieni tak samo na zadaniu. Czasami nie będą uważać i udzielą swojej odpowiedzi losowo, takie odpowiedzi są outlierami. Czy jesteśmy w stanie również ten proces zamodelować? Podmienię teraz w danych 40 obserwacji na 0 i 1 przyznane losowo. Następnie zmienię kod modelu tak by postarał się wyestymować czy dana obserwacja pochodzi z modelu logistycznego, czy była losowa.

dat$y[sample(1:401,40)] = sample(0:1,40,replace = T, prob = c(0.5,0.5))

m1 <- "model{
# Likelihood
for (trial in 1:length(y)){
theta_r[trial] = 1/(1+exp(-(stimulus[trial]-100-alpha)/beta))
theta_c[trial] ~ dbern(psi)
z[trial] ~ dbern(fi)
theta[trial] = ifelse(z[trial] == 0,theta_r[trial], theta_c[trial])
y[trial] ~ dbern(theta[trial])
}

# Priors
alpha ~ dnorm(0,1/50^2)
beta ~ dnorm(0,1/100^2)T(0,)
fi ~ dbeta(1,1)
psi ~ dbeta(1,1)
}"


# what parameters we want to track
params = c("alpha", "beta", "fi", "psi","z")
# compile model
jmod = jags.model(file = textConnection(m1), data = as.list(dat,nTrials),
n.chains = 4, inits = NULL, n.adapt = 100, quiet = T)
# iterate through jmod for the extent of the burn-in
update(jmod, n.iter=1000, by=1)
# draw samples from the posterior for params
post = coda.samples(jmod, params, n.iter = 4000, thin = 1)
# diagnostic evaluation of posterior samples
MCMCsummary(post, params = c("alpha", "beta","fi","psi"))[,1:6]

           mean         sd        2.5%       50%     97.5% Rhat
alpha 0.1893940 1.74895586 -3.17769892 0.1587746 3.7167300 1.02
beta  6.3105011 1.55820164  3.74303655 6.1531747 9.7781392 1.00
fi    0.1059453 0.03749241  0.03508879 0.1054297 0.1819927 1.00
psi   0.5435590 0.15292813  0.26600019 0.5318289 0.8825876 1.07

Model poradził sobie nieźle. Parametr fi mówi nam o odsetku outlierów wyestmowanych przez model. Parametr psi wkazuje natomiast jakie jest prawdopodobieństwo, że outlier przyjmie wartość 1.

Możemy także sprawdzić jakie prawdopodobne jest, że dana obserwacja jest outlierem.

z = MCMCsummary(post, params = c("z"))[,1:6]
head(z)

          mean        sd 2.5% 50% 97.5% Rhat
z[1] 0.0542500 0.2265174    0   0     1 1.00
z[2] 0.0528750 0.2237909    0   0     1 1.00
z[3] 0.0540000 0.2260248    0   0     1 1.00
z[4] 0.9711875 0.1672845    0   1     1 1.02
z[5] 0.0562500 0.2304111    0   0     1 1.00
z[6] 0.0545000 0.2270087    0   0     1 1.00

Ot, stworzyliśmy właśnie model poznawczy dyskryminacji bodźca, biorący pod uwagę procesy uwagowe badanageo (skupienie na zadaniu). Więcej o bayesowskim modelowaniu krzywej psychometrycznej możecie przeczytać tutaj (Lee, 2018).