Dzisiejszy wpis będzie krótki. Pokażę wam jak zrobić to co robiliśmy w poprzedniej części przy użyciu oprogramowania, które pozwoli nam na tworzenie i estymowanie (przy użyciu MCMC) nawet bardzo skomplikowanych modeli w łatwy sposób. Możliwości jest kilka, ja przedstawie wam JAGS (Just Another Gibbs Sampler). Jest to samodzielne oprogramowanie, które można używać bezpośrednio lub za pomocą języków programowania takich jak R, a także graficznego programu statystycznego JASP. Pobrać możecie go tutaj.
JAGS
Powtórzmy naszą bayesowską regresję z tym razem przy użyciu JAGS. Stwórzmy zbior danych:
Musimy zdefiniować kod naszego modelu. JAGS używa dosyć intuicyjnego kodowania BUGS. Model regresji będzie wyglądał tak:
mod = "model {
# Priors
a ~ dunif(-1000, 1000)
b ~ dnorm(0, 100^-2)
sigma ~ dunif(0.000001,1000)
# Likelihood
for (i in 1:length(y)) {
y[i] ~ dnorm(a + b * x[i], sigma^-2)
}}"Operator ~ oznacza, że parametr po lewej stronie dany jesr rozkładem po prawej. Ponieważ w naszym kodzie tylko zmienna Y występuje w danych, JAGS automatycznie rozpozna, że zdefiniowany rozkład Y jest funkcją wiarygodności. Zauważcie, że gdy definuje b jako wartość losowaną z rozkładu normalnego \(N(0,100)\), jako drugi argument podałem \(100^{-2}\). JAGS zamiast odchylenia standardowego dla rozkładu normalnego przyjmuje precyzję (precision), czyli odwrotność wariancji. Po więcej szczegółów polecam zajrzeć do dokumentacji.
# Parametry, które chcemy śledzić.
params = c("a","b","sigma")
## Hiperparametry
n.adapt = 100
# Liczba iteracji adaptacji
ni = 3000
# Liczba iteracji "wypalania"
nb = 3000
# Liczba próbek z rozkładu post priori
nt = 1
# Odchudzanie - 1 oznacza, bierzemy każdą próbkę z rozkładu post priori
nc = 3
# liczba łańcuchów
# Inicjacja modelu
jmod = jags.model(file = textConnection(mod), data = data, n.chains = nc, inits = NULL, n.adapt = n.adapt)Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph information:
Observed stochastic nodes: 100
Unobserved stochastic nodes: 3
Total graph size: 412
Initializing model# Wypalanie
update(jmod, n.iter=ni, by=1)
# Losowanie próbek z rozkładu post priori
post = coda.samples(jmod, params, n.iter = nb, thin = nt)Zauważcie, że Jags miał tylko 3000 iteracji wypalania, podczas gdy mój kod z poprzedniej części potrzebował ponad 16 razy więcej. JAGS używa kombinacji różnych agorytmów MCMC, ponado dokonuje za nas tunningu hiperparametrów (takich jak na przykład step size w Metropolis-Hasting). Dlatego, oprócz wypalania i losowania, mamy jeszcze adaptację. Obejrzmy sobie rozkłady post priori:
plot(post)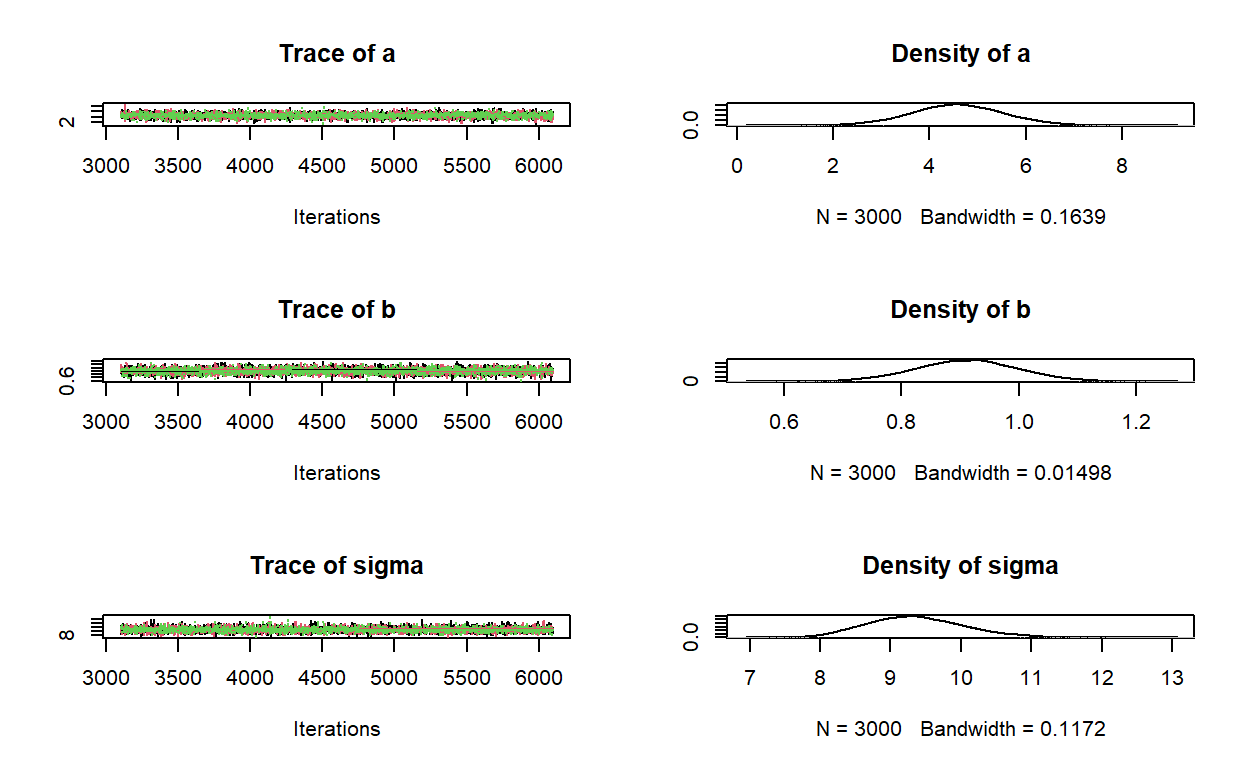
Policzmy statystyki:
summary(post)
Iterations = 3101:6100
Thinning interval = 1
Number of chains = 3
Sample size per chain = 3000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
a 4.5803 0.95620 0.010079 0.010650
b 0.9113 0.08775 0.000925 0.000925
sigma 9.3601 0.68294 0.007199 0.007507
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
a 2.702 3.9454 4.5744 5.2252 6.471
b 0.738 0.8524 0.9122 0.9695 1.085
sigma 8.148 8.8782 9.3262 9.7982 10.810A także sprawdźmy czy łańcuchy się zbiegły:
gelman.diag(post)Potential scale reduction factors:
Point est. Upper C.I.
a 1 1
b 1 1
sigma 1 1
Multivariate psrf
1Statystyka Gelmana-Rubina wskazuje, że łańcuchy się zbiegły. Sprawdźmy jeszcze czy aby na pewno stastystyka nie osiągneła takich wartości przez przypadek.
gelman.plot(post)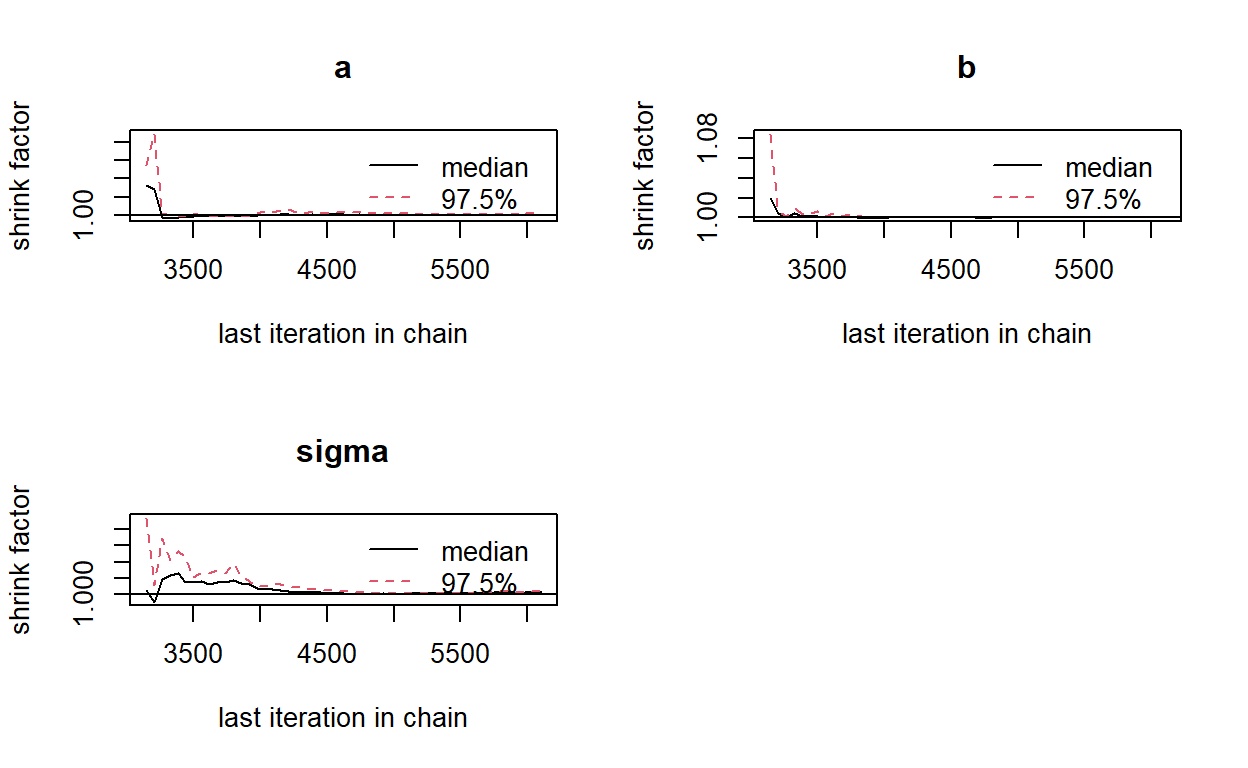
Na wykresie widzimy statystykę Gelmana Rubina liczną dla każdych 50 iteracji następujących po sobie. Dzięki temu możemy sprawdzić czy nasze próby wylosowane są z rozkładów, które naprawdę się zbiegły. Widzimy, że dla początkowych wartości łancuchów statystyka ma wyższe wartośći, co może sugerować, że powinniśmy zastosować dłuższy interwał wypalania (choć w naszym przypadku statystyka nie przekracza nigdzie wartości 1.15, więc bybyłby to raczej zabieg kosmetyczny).
Sprawdźmy autokorelację:
autocorr.diag(post) a b sigma
Lag 0 1.000000000 1.000000000 1.000000000
Lag 1 0.029878333 0.021306509 0.050087619
Lag 5 0.005264560 -0.002882478 0.003968644
Lag 10 0.002108300 -0.009317490 0.006910744
Lag 50 0.006366223 0.019776605 -0.017047426Autokorelacja praktycznie nie występuje.
JAGS poradził sobie dużo lepiej z regresją liniową, niż mój zabawkowy kod.Ponadto jego składnia jest relatywnie prosta. Dlatego z niego będziemy korzystać w następnych częściach tutorialu.
Przykładowe kody JAGS dla wielu modeli możecie znaleść tutaj.
JAGS in JASP
Jeśli ktoś nie jest wielkim fanem robienia statystyk za pomocą języków programowania, JAGS jest kompatybilny z graficznym programem statystycznym JASP.
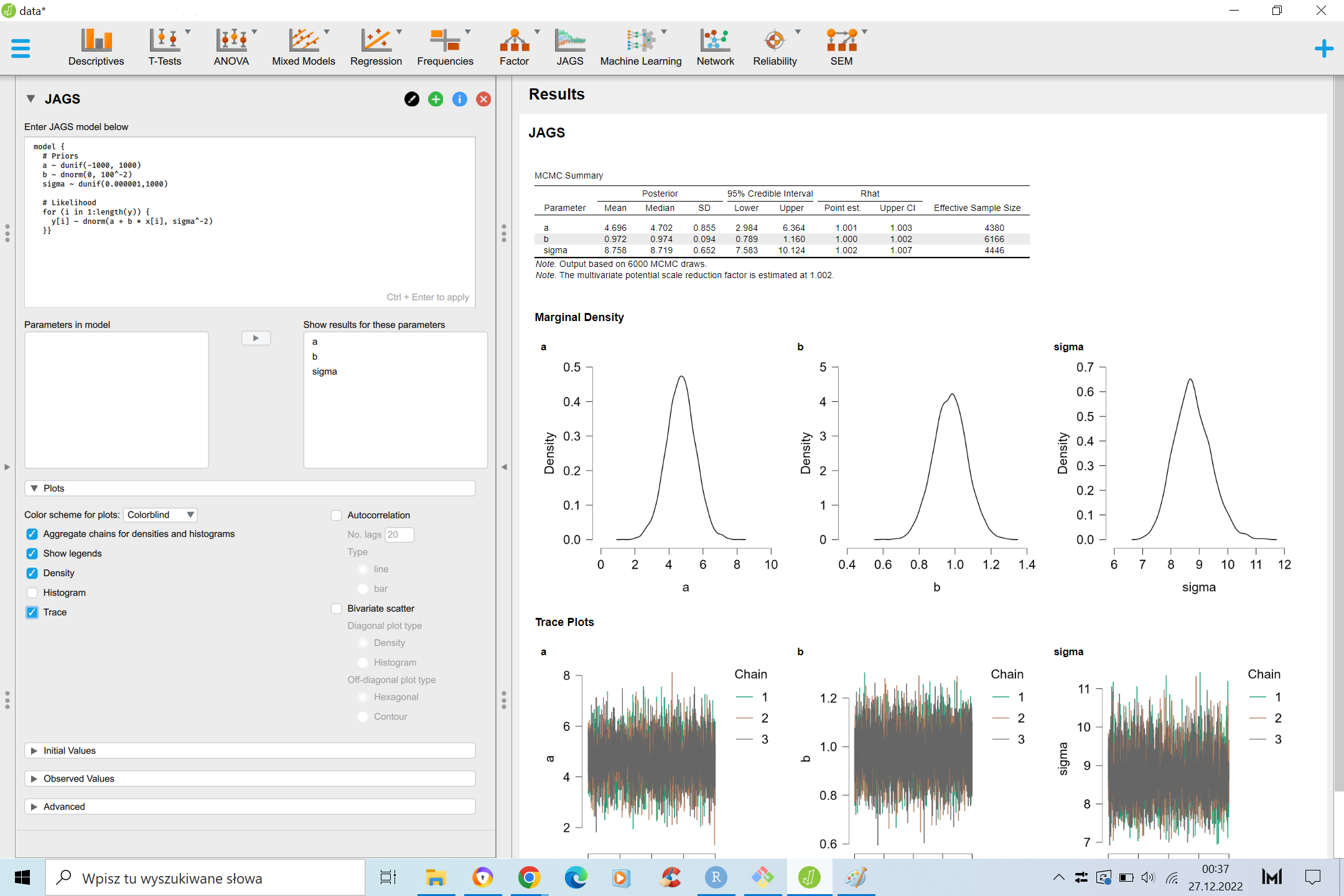
Bonus - diagramy Bayesowskie
Warto wspomnieć, że do wizualizacji modeli bayesowskich często używa się grafów (ja do ich budowy używam biblioteki daft w Pythonie). W przypadku naszego modelu:
import daft
import matplotlib.pyplot as plt
pgm = daft.PGM(observed_style="inner")
pgm.add_node("alpha", r"$\alpha$", 0.5, 2)
pgm.add_node("beta", r"$\beta$", 1.5, 2)
pgm.add_node("sigma", r"$\sigma$", 2.5, 2)
pgm.add_node("x", r"$x_i$", 2, 1, observed=True)
pgm.add_node("y", r"$y_i$", 1, 1, observed=True)
pgm.add_edge("alpha", "y")
pgm.add_edge("beta", "y")
pgm.add_edge("x", "y")
pgm.add_edge("sigma", "y")
pgm.add_plate([0.5, 0.5, 2, 1], label=r"$i = 1, \ldots, N$", shift=-0.1)
pgm.render()
plt.show() 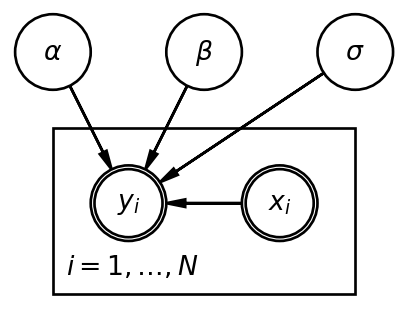
Diagram pokazuje, że rozkład zmiennej \(y_i\) definują 3 nieobserwowalne parametry (pojedyńcze okręgi) i jedna obserwowalna zmienna (pogrubiony okrąg).
W przypadku modeli bayesowskich zapewno dosyć często będziecie się spotykać z takimi graficznymi opisami modeli. Do grafu dołączane są zwykle definicje parametrów. W naszym przypadku:
\[\alpha \sim U(-1000, 1000)\] \[ \beta \sim N(0, 100) \] \[ \sigma \sim U(0.000001,1000)\] \[ y_i \sim N(a + b * x_i, \sigma)\]