Dzisiejszy wpis będzie taką mini motywacją do zainteresowania się mieszanymi modelami liniowymi (aka hierarchicznymi/wielopoziomowymi modelami liniowymi).
Rozważmy hipotetyczny eksperyment. Badane osoby oglądają różne zdjęcia, a po po obejrzeniu oceniają jak bardzo zdjęcie było pobudzające. W trakcie badania uczesnicy mają na palcu wskazującym i środkowym elektrody mierzące aktywność skórno-galwaniczną (mikropocenie).
Następnie możemy zadać pytanie czy większa amplituda sygnału z elektrod jest związana z większym pobudzeniem. Jeśli pytamy o to, czy osoby z średnio wyższą amplitudą sygnału mają wyższą średnią ocenę (efekt międzyobiektowy), możemy po prostu uśrednić pomiary na osobę i skorelować je ze sobą.
Jeśli jednak zapytamy czy średnio im większy sygnał w pojedynczym pomiarze, tym wyższa ocena (efekt wewnątrzobiektowy), takie podejście może nie zadziałać. Czemu? Zasymulujmy sobie takie dane.
library(tidyverse)
library(lme4)
library(parameters)
library(datawizard)
library(cowplot)
between_effect = 0
within_effect = 0.5
between_sd = 2
within_sd = 0.1
signal_intercepts = rnorm(100,0,1)
response_intercepts = rnorm(100,0, between_sd) + between_effect * signal_intercepts
data = data.frame()
for (participant in 1:100){
signal = rnorm(100,4,0.1)
response = within_effect*signal + rnorm(100,0,within_sd)
response = response + response_intercepts[participant]
signal = signal + signal_intercepts[participant]
data = rbind(data, data.frame(signal,response,participant))
}
data_averaged = data %>% group_by(participant) %>% summarise(mean_signal = mean(signal), mean_response = mean(response))
cat("Korelacja pojedynczych pomiarów",cor(data$signal, data$response))
Korelacja pojedynczych pomiarów -0.0215814cat("Korelacja średnich pomiarów na osobę",cor(data_averaged$mean_signal, data_averaged$mean_response))
Korelacja średnich pomiarów na osobę -0.02477697Nie obserwujemy znaczących korelacji w żadnym wypadku. Zerknięcie na wykres wyjaśni tajemnicę:
plot1 <- ggplot(data, aes(x = signal, y = response, colour =
as.character(participant))) + geom_point() + theme_bw() +
theme(legend.position="none")
plot2 <- ggplot(data_averaged, aes(x = mean_signal, y = mean_response)) +
geom_point() + theme_bw()
plot_grid(plot1, plot2, labels = "AUTO")
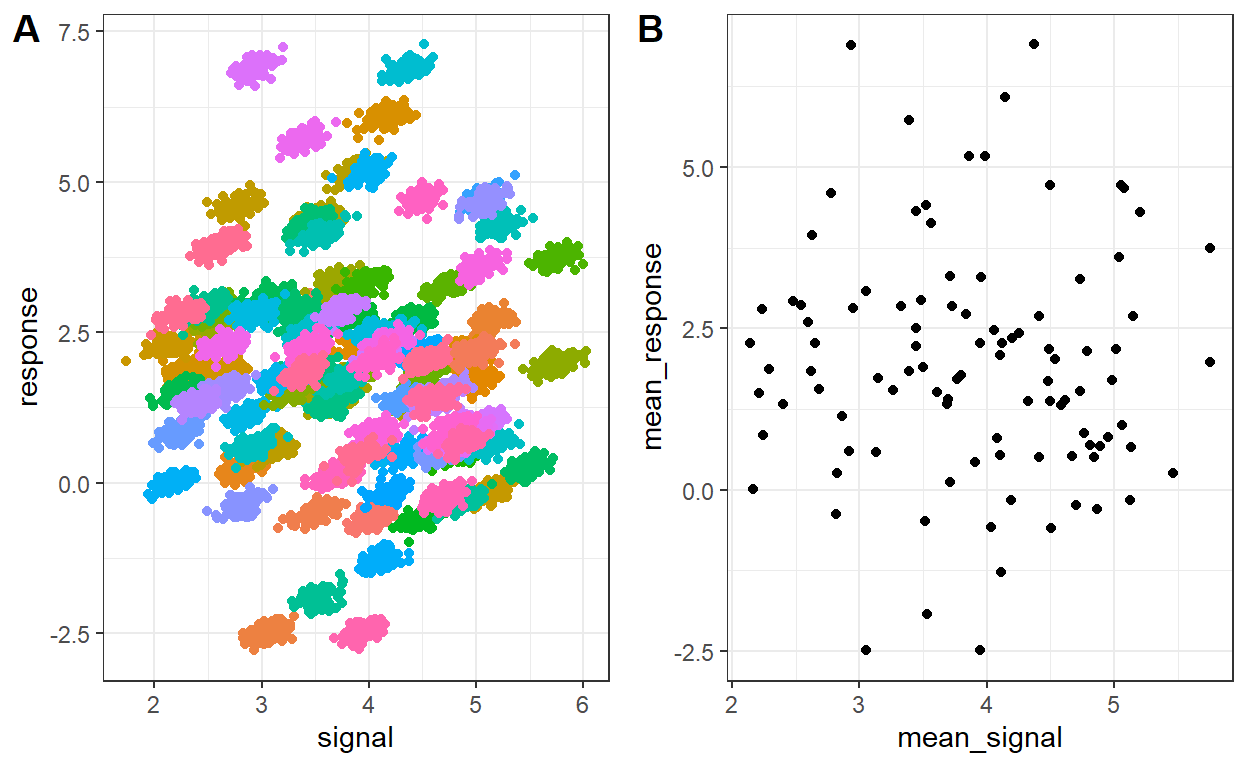
Jeśli spojrzymy na wykres po lewej, zobaczymy różnokolorowe zgrupowane punkty. Te kolory to poszczególni badani. Jeśli się im przyjrzymy zauważymy, że są lekko przechylone w prawo, co sugeruje związek liniowy. Jednak badani są rozrzuceni po całym wykresie (duża wariancja międzyobiektowa), ponieważ występuje duże zróżnicowanie pomiędzy ich bazowymi amplitudami i ocenami. Wykres ich średnich pokazuje brak związku, ponieważ te bazowe wartości nie są ze sobą związane. Jak więc wykryć związek?
A gdybyśmy tak od wartości naszych zmiennych odjęli średnią dla danego badanego?
data = data %>% group_by(participant) %>% mutate(signal_demeaned = signal - mean(signal),
response_demeaned = response - mean(response))
ggplot(data, aes(x = signal_demeaned, y = response_demeaned, colour = as.character(participant))) +
geom_point() + theme_bw() + theme(legend.position="none")
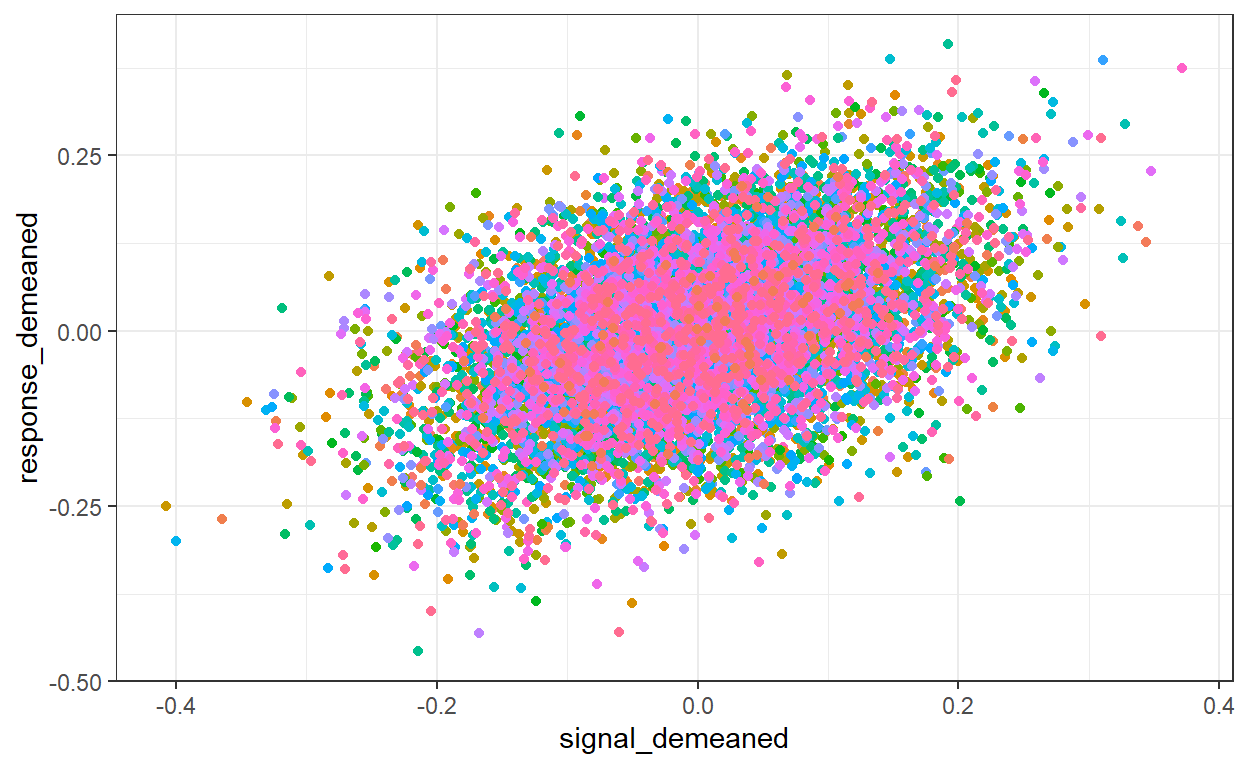
Lepiej, co nie? Jak więc uwzględnić to w modelu liniowym?
Regresja liniowa ma postać:
\[ Y_i = \alpha + \beta X_i\] gdzie \(a\) to stała, a \(\beta\) to współczynnik regresji.
Nasz model musimy zmodyfikować tak by brał pod uwagę średnie amplitudy badanych.
\[ Y_{ij} = \alpha + \beta X_i + b_j z_i\]
gdzie \(z_j\) to zmienna binarna oznaczająca czy dany pomiar należy do badanego \(j\), a \(b_j\) to współczynnik regresji dla \(z_j\). Ponieważ \(z_i\) przyjmuje dla badanego \(j\) wartość 1, a dla wszystkich innych 0, równanie możemy przepisać:
\[ Y_{ij} = (\alpha +b_j) + \beta X_i\] Jak widzimy teraz nasz model uwzględnia odchylenia od stałej dla każdego badanego.
Zerknijmy na model mieszany:
model = lmer(response ~ signal + (1| participant), data = data)
model_parameters(model)
# Fixed Effects
Parameter | Coefficient | SE | 95% CI | t(9996) | p
-------------------------------------------------------------------
(Intercept) | -0.02 | 0.19 | [-0.40, 0.36] | -0.09 | 0.926
signal | 0.51 | 0.01 | [ 0.49, 0.52] | 50.43 | < .001
# Random Effects
Parameter | Coefficient
-----------------------------------------
SD (Intercept: participant) | 1.89
SD (Residual) | 0.10W tabeli Fixed Effects mamy estymaty stałej \(a\) i współczynnika regresji \(\beta\). Niżej w tabeli Random Effects widzimy estymaty odchylenia standardowego stałych \(b\) (wariancji międzyobiektowej) i błędu (w tym wypadku wariancji wewnątrzobiektowej). Jak widzimy współczynnik dla sygnału jest pozytywny i wynosi około 0.5. Dzięki dodaniu dodatkowych stałych \(b_j\) nasz model liczy teraz efekt wewnątrzobiektowy.
Ale czasami chcielibyśmy by liczył także efekt międzyobiektowy. Spójrzmy na taki przykład:
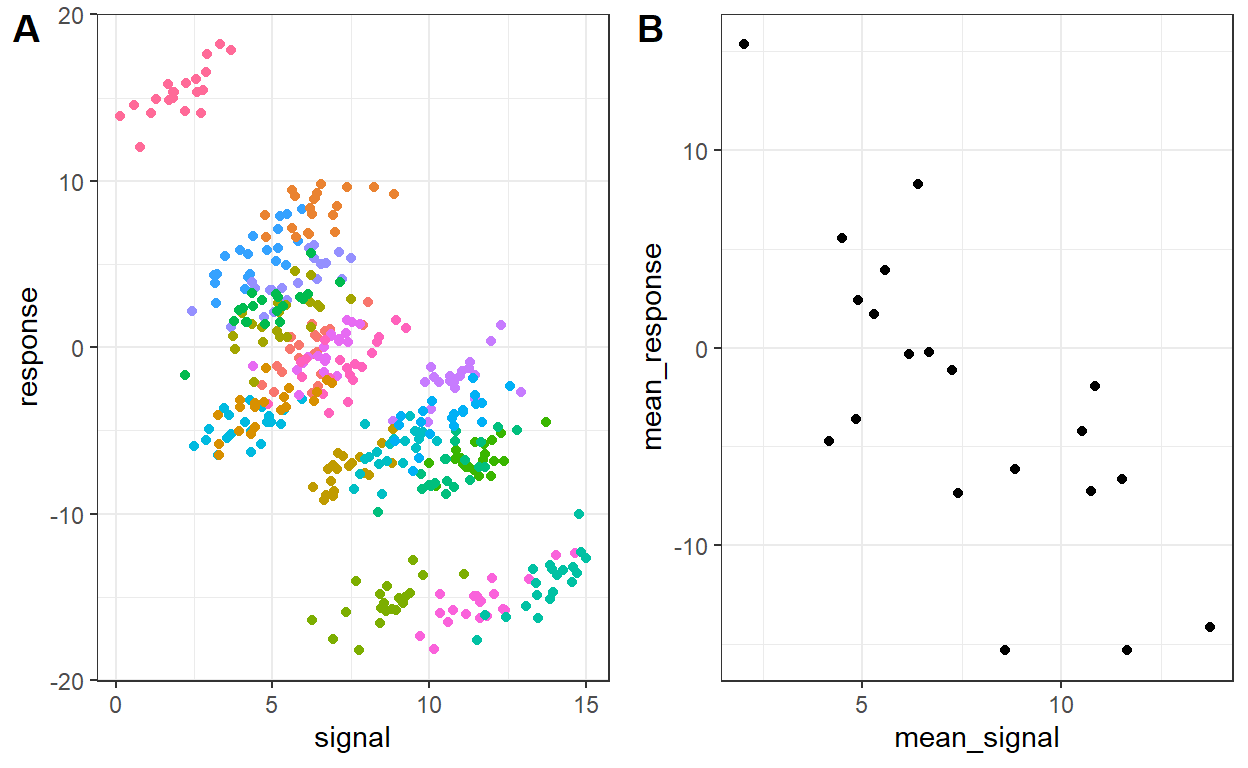
Jak widzimy na wykresie, występuje zarówno efekt międzyobiektowy, jak i wewnątrzobiektowy. Ponadto, te efekty mają przeciwny znak.
Przykładem z życia takiej sytuacji jest szybkość pisania na klawiaturze. Im szybciej średnio dana osoba pisze na klawiaturze tym rzadziej popełnia błędy. Jednak każda osoba, im relatywnie szybciej (względem swojej średniej) pisze, tym więcej błędów popełnia.
Model mieszany wykryje tylko efekt wewnątrzobiektowy. Jeśli chcielibyśmy wykryć oba efekty, musimy wykonać pewną sztuczkę i rozbić zmienną niezależną na dwie (Bell et al., 2019): \(X_{between}\) = średnia dla danego badanego i \(X_{within} = X - X_{between}\).
data <- cbind(
data,
demean(data, select = c("signal"), group = "participant")
)
model = lmer(response ~ signal_within + signal_between + (1| participant), data = data)
model_parameters(model)
# Fixed Effects
Parameter | Coefficient | SE | 95% CI | t(395) | p
----------------------------------------------------------------------
(Intercept) | 11.71 | 3.19 | [ 5.44, 17.99] | 3.67 | < .001
signal within | 0.93 | 0.05 | [ 0.83, 1.03] | 17.86 | < .001
signal between | -1.88 | 0.39 | [-2.65, -1.11] | -4.81 | < .001
# Random Effects
Parameter | Coefficient
-----------------------------------------
SD (Intercept: participant) | 5.27
SD (Residual) | 1.00Dzięki temu nasz model estymuje zarówno efekt wewnątrzobiektowy, jak i międzyobiektowy.
Poniżej możecie zobaczyć jak zmiana poszczególnych parametrów w symulacji (kod z początku wpisu) wpływa na to jak wyglądają dane i jak radzi sobie model mieszany.
Możliwość estymacji efektów wewnątrzobiektowych i międzyobiektowych to jedna z zalet mieszanych modeli liniowych. Posiadają one jeszcze inne, ciekawe właściwości. Niemniej, tu zakończymy tą małą zachętę do stosowania mieszanych modeli liniowych.
Jeśli ktoś jest zainteresowany szczegółami, zarówno matematycznymi jak i bardziej praktycznymi, zachęcam do skorzystania z bazy wiedzy, gdzie znajdują się odnośniki do dobrych tutoriali i kursów omawiających tę klasę modeli.